Comentários / Receita Federal do Brasil - Auditor Fiscal da Receita Federal - ESAF - 2012 - Prova 1
Questão:
A função bijetora dada por f(x) = 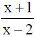
|
|
a)
f -1 (x) = |
|
|
b)
f -1 (x) = |
|
|
c)
f -1 (x) = |
|
|
d)
f -1 (x) = |
|
|
e)
f -1 (x) = |
Comentários
- 01/03/2017 / 12:03Seja y=f(x)
. Então:
y=x+1x−2
Isolando x:
(x−2)y=x+1
xy−2y=x+1
xy−x=1+2y
x(y−1)=1+2y
x=1+2yy−1
Trocando x por f−1(x)
e y por x, temos:
f−1(x)=1+2xx−1
Resposta: A
Deixe o seu comentário aqui
Para comentar você precisa estar logado.
Copyright © Tecnolegis - 2010 - 2025 - Todos os direitos reservados.
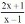 de R - {1} em R - {2}.
de R - {1} em R - {2}.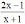 de R - {1} em R - {2}.
de R - {1} em R - {2}.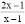 de R - {2} em R - {1}.
de R - {2} em R - {1}.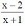 de R - 1 em R - {2}.
de R - 1 em R - {2}.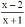 de R - 2 em R - {1}.
de R - 2 em R - {1}.