Comentários / ENADE (Exame Nacional de Desempenho de Estudantes) - Engenheiro - INEP (Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira) - 2017

Questão:

A importância da otimização no processo produtivo é inegável. Do ponto de vista matemático, para otimizar determinada grandeza, é necessário modelá-la de acordo com uma função e, a partir daí, conforme a situação, procurar um máximo ou um mínimo. Uma das formas usadas para minimizar funções é o método dos multiplicadores de Lagrange.

Um fabricante de latinhas de refrigerante deve propor uma lata cilíndrica de volume V₀. Essa lata será fabricada usando-se duas ligas metálicas distintas, sendo uma para a parte lateral e outra para a base e a tampa. Ele deseja calcular o raio (r) e a altura (h) da lata para que o custo de sua produção seja o menor possível. Sabe-se que a área total da lata é dada por A(r,h) e que o custo total de produção da lata, que depende apenas do material utilizado na sua produção, é C(r,h). Para a solução desse problema, será utilizado o método dos multiplicadores de Lagrange.

Com base nessa situação, avalie as afirmações a seguir, acerca da solução desse problema.

I. O custo de produção da lata pode ser expresso por C( r, h) = 2 π (K₁ rh + K₂r ²), em que K₁ e K₂ são constantes que dependem do custo de cada uma das ligas metálicas por unidade de área.

II. A função a ser minimizada da área total da lata é A(r,h) = 2 π rh + 2 π r².

III. O vínculo na minimização, relacionado ao volume da lata, é dado por g(r,h) = π r²h-V₀.

IV. O sistema de equações a ser montado é 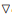C(r,h) = λ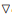g(r,h), no qual λ é denominado multiplicador de Lagrange.

É correto apenas o que se afirma em

a) I e II.

b) I e IV.

c) II e III.

d) I, III e IV.

e) II, III e IV.