Comentários / ENADE (Exame Nacional de Desempenho de Estudantes) - Matemática - INEP (Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira) - 2017
Questão:
A solução de um sistema linear de três equações e três incógnitas pode ser interpretada geometricamente como a interseção de três planos no espaço e consiste em verificar se os três planos têm um único ponto, infinitos pontos ou nenhum ponto em comum, para determinar se o sistema possui solução única, infinitas soluções ou nenhuma solução, respectivamente.
Com base nessas informações, conclui-se que o sistema linear
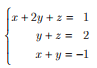
tem como solução
|
|
a)
o ponto (0,-1,3). |
|
|
b)
o plano que passa pelo ponto (0,-1 ,3) e que possui como vetor normal o vetor |
|
|
c)
a reta que passa pelo ponto (0,-1,3) e que possuí como vetor diretor o vetor |
|
|
d)
a reta que passa pelo ponto (0,-1 ,3) e que possuí como vetor diretor o vetor |
|
|
e)
o conjunto vazio. |
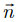 =(1,2,1).
=(1,2,1).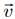 = (1,2,-1).
= (1,2,-1).