ENADE (Exame Nacional de Desempenho de Estudantes) - Matemática - INEP (Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira) - 2017
ENADE (Exame Nacional de Desempenho de Estudantes) - Matemática - INEP (Instituto Nacional de Estudos e Pesquisas Educacionais Anísio Teixeira) - 2017
Considere 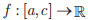 uma função contínua e
uma função contínua e 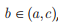 conforme ilustra o gráfico abaixo.
conforme ilustra o gráfico abaixo.
Represente por:
A a área da região limitada pela reta de equação y = 0 e pela curva 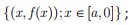
B a área da região limitada pela reta de equação y = 0 e pela curva 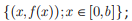
C a área da região limitada pela reta de equação y = 0 e pela curva 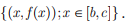
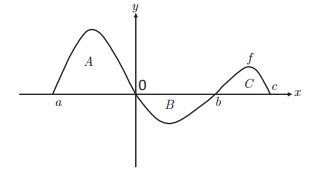
Sabendo-se que A = 5, E = 3 e C = 2, avalie as afirmações a seguir.
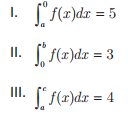
É correto o que se afirma em
|
a) I, apenas.
|
|
b) II, apenas.
|
|
c) I e III, apenas.
|
|
d) II e III, apenas.
|
|
e) I, II e III.
|
Considere uma urna com 5 bolas azuis, 3 verdes e 6 pretas, da qual serão retiradas bolas sem reposição. Com base nessa situação, avalie as afirmações a seguir.
I. Caso sejam retiradas 4 bolas, uma delas será verde.
II. O número mínimo de bolas que devem ser retiradas para se garantir a retirada de uma bola preta é igual a 9.
III. O número mínimo de bolas que devem ser retiradas para se garantir a retirada de uma bola verde e uma bola azul é igual a 10.
É correto o que se afirma em
|
a) II, apenas.
|
|
b) III, apenas.
|
|
c) I e II, apenas.
|
|
d) I e III, apenas.
|
|
e) I, II e III.
|
Considere o cubo de vértices A, B, C, D ,E ,F, G e H, ilustrado na figura abaixo, e os vetores b, c, d, e,f, g e h, todos com origem em A e extremidades respectivamente em B, C, D, E, F, G e H.
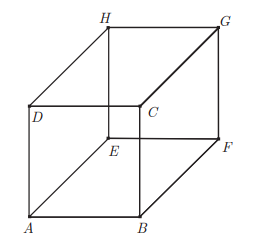
Com base nas informações apresentadas, é correto afirmar que o vetor cujo produto escalar com f é igual a zero é o vetor
|
a) b.
|
|
b) c.
|
|
c) d.
|
|
d) g.
|
|
e) h.
|
Para calcular o limite 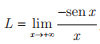 ,os argumentos podem ser desenvolvidos usando as desigualdades
,os argumentos podem ser desenvolvidos usando as desigualdades 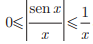 válidas para todo real x > 0.
válidas para todo real x > 0.
A partir desses argumentos, conclui-se que L é igual a
|
a)
-1. |
|
b)
0. |
|
c)
1. |
|
d)
∞. |
|
e)
-∞. |
Uma construtora, com o objetivo de valorizar as áreas verdes, apresentou um projeto de loteamento, com terrenos retangulares, onde cada residência construída terá um jardim ao seu redor. Em cada terreno deverão ser reservados 3 metros na frente, 3 metros no fundo e 2 metros em cada lateral para jardinagem, conforme ilustra a figura a seguir.
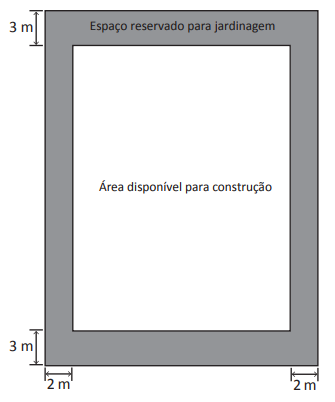
Considerando-se que área disponível para construção será de 600 m2, a área mínima do terreno que atende às especificações exigidas pela construtora será de
|
a)
606 m2. |
|
b)
610 m2. |
|
c)
726 m2. |
|
d)
864 m2. |
|
e)
924 m2. |
A respeito de transformações lineares no plano, avalie as afirmações a seguir.
I. Sabendo que uma transformação de escala é um operador linear no plano cartesiano que multiplica a abscissa x de um ponto por um fator m e sua respectiva ordenada y por um fator n, a matriz associada à transformação de escala que leva, na figura a seguir, o triângulo ABC ao triângulo A 'B 'C' tem determinante igual a 1/2.
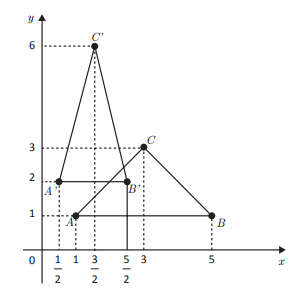
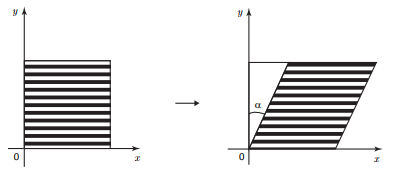
II. A transformação linear que leva a região plana hachurada do gráfico à esquerda na região hachurada do gráfico à direita é dada por T(x,y) = (x,y + x tg α)
III. Na figura a seguir, a matriz da transformação linear que efetua a mudança do triângulo à esquerda para a posição mostrada à direita é 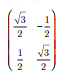
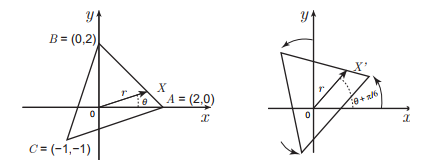
É correto o que se afirma em
|
a) I, apenas.
|
|
b) III, apenas.
|
|
c) I e II, apenas.
|
|
d) II e III, apenas.
|
|
e) I, II e III.
|
O gerente de um posto de combustíveis observou que, na primeira semana do mês em que definiu o preço do litro de gasolina a R$ 3,70, foram vendidos 15 000 litros diários. Com isso, o posto fez uma promoção e percebeu que, para cada centavo de desconto que concedia por litro, eram vendidos 200 litros de gasolina a mais por dia.
Representando por p a quantidade de centavos correspondente ao desconto dado no preço de cada litro de gasolina, e por F o valor, em reais, faturado por dia com a venda de gasolina, a expressão que descreve essa situação é
|
a)
F= 15000 + 590p- 2p2 |
|
b)
F= 15000 + 590p + 2p2 |
|
c)
F= 55500- 590p- 2p2 |
|
d)
F= 55500 + 590p- 2p2 |
|
e)
F = 55 500 - 590p + 2p2 |
A solução de um sistema linear de três equações e três incógnitas pode ser interpretada geometricamente como a interseção de três planos no espaço e consiste em verificar se os três planos têm um único ponto, infinitos pontos ou nenhum ponto em comum, para determinar se o sistema possui solução única, infinitas soluções ou nenhuma solução, respectivamente.
Com base nessas informações, conclui-se que o sistema linear
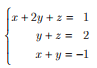
tem como solução
|
a)
o ponto (0,-1,3). |
|
b)
o plano que passa pelo ponto (0,-1 ,3) e que possui como vetor normal o vetor |
|
c)
a reta que passa pelo ponto (0,-1,3) e que possuí como vetor diretor o vetor |
|
d)
a reta que passa pelo ponto (0,-1 ,3) e que possuí como vetor diretor o vetor |
|
e)
o conjunto vazio. |
Considere o conjunto 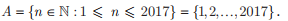
O número de elementos de A que são múltiplos de 4 ou 6 é igual a
|
a) 840.
|
|
b) 756.
|
|
c) 672.
|
|
d) 168.
|
|
e) 84.
|
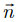 =(1,2,1).
=(1,2,1).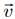 = (1,2,-1).
= (1,2,-1).