FGV - Fundação Getúlio Vargas - Vestibular - FGV - Fundação Getúlio Vargas - 2012 - Primeira Fase - 1.º Semestre - 2013 - Rio de Janeiro
José comprou um imóvel por R$ 120.000,00 e o vendeu por R$ 140.000,00. Algum tempo depois, recomprou o mesmo imóvel por R$ 170 000,00 e o revendeu por R$ 200 .000,00.
Considerando-se apenas os valores de compra e venda citados, José obteve um lucro total de
|
a)
R$ 200 000,00 |
|
b)
R$ 80 000,00 |
|
c)
R$ 50 000,00 |
|
d)
R$ 30 000,00 |
|
e)
R$ 20 000,00 |
Uma caixa sem tampa é construída a partir de uma chapa retangular de metal, com 8 dm de largura por 10 dm de comprimento, cortando-se, de cada canto da chapa, um quadrado de lado x decímetros e, a seguir, dobrando-se para cima as partes retangulares, conforme sugere a figura a seguir:
O volume, em dm3, da caixa assim obtida é
|
a)
80x -36x2 + 4x3. |
|
b)
80x +36x2 + 4x3. |
|
c)
80x -18x2 + x3. |
|
d)
80x +18x2 + x3. |
|
e)
20x -9x2 + x3. |
Sejam x , y ,z e w números inteiros tais que x < 2y , y < 3z e z < 4w.
Se w <10, então o maior valor possível para x é
|
a)
187. |
|
b)
191. |
|
c)
199. |
|
d)
207. |
|
e)
213. |
Os vértices de um cubo são pintados de azul ou de vermelho. A pintura dos vértices é feita de modo que cada aresta do cubo tenha pelo menos uma de suas extremidades pintada de vermelho.
O menor número possível de vértices pintados de vermelho nesse cubo é
|
a)
2. |
|
b)
3. |
|
c)
4. |
|
d)
6. |
|
e)
8. |
Em uma corrida em que não há empates, há apenas três competidores: A, B e C. A chance de A ganhar é de 1- para -3 . A chance de B ganhar é de 2- para -3 .
Sabe-se que a expressão “a chance de X ganhar é de p - para -q ” significa que a probabilidade de X ganhar é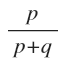 
.
A chance de C ganhar é de
|
a)
0 - para-3. |
|
b)
3- para-3. |
|
c)
5- para-12. |
|
d)
7 - para-13. |
|
e)
13- para -20. |
Em uma urna há bolas verdes e bolas amarelas. Se retirarmos uma bola verde da urna, então um quinto das bolas restantes é de bolas verdes. Se retirarmos nove bolas amarelas, em vez de retirar uma bola verde, então um quarto das bolas restantes é de bolas verdes.
O número total de bolas que há inicialmente na urna é
|
a)
21. |
|
b)
36. |
|
c)
41. |
|
d)
56. |
|
e)
61. |
Um quadrado é dividido em quatro retângulos congruentes traçando-se três linhas paralelas a um dos lados, conforme a figura.
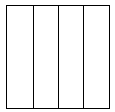
Se a área de cada um desses quatro retângulos é 48 cm2, então o perímetro, em centímetros, do quadrado original é
|
a)
64. |
|
b)
48 √3. |
|
c)
48 √2. |
|
d)
32 √3. |
|
e)
32 √2. |
Um pesquisador fez um conjunto de medidas em um laboratório e construiu uma tabela com as frequências relativas (em porcentagem) de cada medida, conforme se vê a seguir:
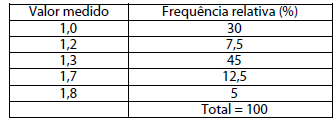
Assim, por exemplo, o valor 1,0 foi obtido em 30% das medidas realizadas. A menor quantidade possível de vezes que o pesquisador obteve o valor medido maior que 1,5 é
|
a)
6. |
|
b)
7. |
|
c)
8. |
|
d)
9. |
|
e)
10. |
No restaurante italiano Ingiusto, os garçons colocam os pedidos dos clientes à cozinha uns sobre os outros de modo que eles formam uma pilha de pedidos. Cada novo pedido que chega é colocado no topo da pilha. O pessoal da cozinha, quando se vê livre para pegar um novo pedido, pega sempre o pedido que está no topo da pilha.
Em determinado dia, durante a primeira hora de funcionamento do restaurante, foram feitos e atendidos quatro pedidos de clientes. Suponha que eles tenham sido numerados e que foram colocados na pilha, na ordem 1, 2, 3, 4.
Das sequências a seguir, aquela que pode representar a ordem em que esses pedidos foram pegos pelo pessoal da cozinha é
|
a)
1, 3, 2, 4. |
|
b)
2, 4, 1, 3. |
|
c)
4, 2, 1, 3. |
|
d)
3, 4, 1, 2. |
|
e)
4, 1, 2, 3. |
Maria fez um empréstimo bancário a juros compostos de 5% ao mês. Alguns meses após ela quitou a sua dívida, toda de uma só vez, pagando ao banco a quantia de R$ 10 584,00.
Se Maria tivesse pago a sua dívida dois meses antes, ela teria pago ao banco a quantia de
|
a)
R$ 10 200,00. |
|
b)
R$ 9 800,00. |
|
c)
R$ 9 600,00. |
|
d)
R$ 9 200,00. |
|
e)
R$ 9 000,00. |