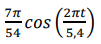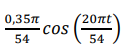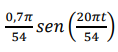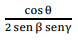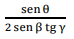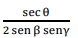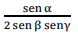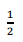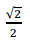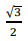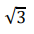IF-PB (Instituto Federal de Educação, Ciência e Tecnologia da Paraíba) - Professor EBTT - Matemática - IDECAN (Instituto de Desenvolvimento Educacional, Cultural e Assistencial Nacional) - 2019
Se um objeto for lançado na vertical, de baixo para cima, em um determinado planeta e seu movimento for governado pela seguinte função y(t) = 10t – 1,86t², calcule a taxa de variação da posição com relação ao tempo após 2 (dois) segundos.
|
a) 1,86 m/s
|
|
b) 2,56 m/s
|
|
c) 6,28 m/s
|
|
d) 10 m/s
|
|
e) 12,56 m/s
|
Uma empresa produz peças de madeira com tamanho fixo. A quantidade Q de cada peça de madeira, dada em metros, vendida é função do preço P em real por metro. Desta forma, podemos afirmar que a receita das vendas conseguida com o preço de venda P é igual a R(P) = Pf (P). Sabendo-se ainda que f(20) = 10.000,00 e f'(20) = -350,00, calcule o valor de R'(20).
|
a) R$ 1.000,00
|
|
b) R$ 3.000,00
|
|
c) R$ 7.000,00
|
|
d) R$ 13.000,00
|
|
e) R$ 17.000,00
|
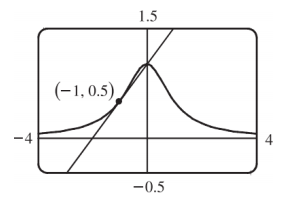
A função y(x) = 1/(1+x²) é responsável pela construção da curva abaixo em formato de sino. Calcule o valor do par ordenado da reta tangente que toca o eixo x na parte negativa do gráfico.
|
a) (-2, 1)
|
|
b) (-1, 1)
|
|
c) (-0.5, 0)
|
|
d) (-1.5, 0)
|
|
e) (-2, 0)
|
O brilho médio de uma lâmpada fluorescente é dado pela seguinte função abaixo:
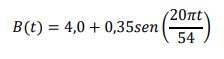
Calcule a função de taxa de variação do brilho após t dias.
|
a)
|
|
b)
|
|
c)
|
|
d)
|
|
e)
g |
Dado um λ suponha que o mesmo é autovalor de A invertível e que µ é autovalor de B com mesmo autovetor ū. Calcule o autovalor associado ao autoveto ū de A2.
|
a)
λ2 |
|
b)
λ |
|
c)
1 − λ |
|
d)
1 − λ2 |
|
e)
− λ2 |
Uma série de potência pode ser dada de acordo com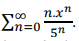 
. Calcule o(s) valor(es) de x para o(s) qual(is) a série de potência é convergente.
|
a) A série converge para um intervalo aberto (-5, 5).
|
|
b) A série converge para um intervalo fechado (-5, 5).
|
|
c) A série converge para o valor de x = 5.
|
|
d) A série converge para o valor de x = -5.
|
|
e) A série converge para x > 5.
|
Considere que tenhamos uma equação diferencial na forma dada como M (x,y)dx + N (x,y)dy = 0. As funções podem ser escritas como M (x,y) = f(x)g(y) e N (x,y) = F(x)G(y). A equação M(x,y)dx + N(x,y)dy = 0 pode ser considerada
|
a)
uma equação de Riccati. |
|
b)
uma equação diferencial separável. |
|
c)
uma equação diferencial não-separável. |
|
d)
uma equação de Bernoulli de ordem superior. |
|
e)
uma equação diferencial de segunda ordem. |
Do ponto médio dos lados AB e AC de um triângulo ABC traçamse retas que se cortam num ponto M do terceiro lado BC e que formam com este lado ângulos iguais, cujo valor é θ.
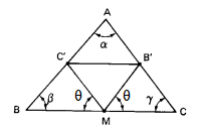
A cotg θ é igual a
|
a)
|
|
b)
|
|
c)
|
|
d)
|
|
e)
|
Determine a equação da curva gerada por um ponto que se move de modo que a sua distância ao ponto (−1, 3) seja igual à sua distância à reta y + 3 = 0.
|
a)
y2 + 2y − 6x + 1 = 0 |
|
b)
x2 + 2x − 12y + 1 = 0 |
|
c)
2x2 + 4x − 12y + 1 = 0 |
|
d)
y2 + 12y − 6x + 1 = 0 |
|
e)
x2 + 2y − 6x + 1 = 0 |
