Texto - Lógica - TRT5

Na comunicação, o elemento primitivo é a sentença, ou proposição simples, formada basicamente por um sujeito e um predicado. Nessa definição, estão incluídas apenas as proposições afirmativas ou negativas, excluindo-se, portanto, as proposições interrogativas, exclamativas etc. São consideradas proposições somente aquelas sentenças bem definidas, isto é, aquelas acerca das quais é possível decidir serem verdadeiras (V) ou falsas (F). Toda proposição tem um valor lógico, ou uma valoração, V ou F, excluindo-se qualquer outro valor. As proposições são designadas por letras maiúsculas A, B, C etc. A partir de determinadas proposições, denominadas proposições simples, podem ser formadas novas proposições, empregando-se os seguintes conectivos: “e”, indicado por ∧; “ou”, indicado por ∨; “se ... então”, indicado por →; “se ... e somente se”, indicado por ↔. A relação A↔B significa (A→B)∧(B→A). Emprega-se também o modificador “não”, indicado por ¬. Se A e B são duas proposições, constroem-se as tabelas-verdade das proposições compostas formadas a partir das proposições simples A e B, dos conectivos e do modificador citados — a coluna correspondente a determinada proposição composta é a tabela-verdade daquela proposição —, conforme apresentado a seguir.

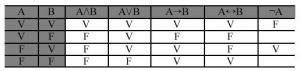
Há expressões às quais não se pode atribuir um valor lógico V ou F, por exemplo: “Ele é juiz do TRT da 5.ª Região”, ou “x + 3 = 9”. Nessas expressões, o sujeito é uma variável e pode ser substituído por um elemento arbitrário, transformando a expressão em uma proposição que pode ser valorada como V ou F. Expressões dessa forma são denominadas sentenças abertas, ou funções proposicionais.

Pode-se passar de uma sentença aberta a uma proposição por meio dos quantificadores “qualquer que seja”, ou “para todo”, indicado por ∀, e “existe”, indicado por ∃. Por exemplo: a proposição (∀x)(x ∈ R)(x + 3 = 9) é valorada como F, ao passo que a proposição (∃x)(x ∈ R)(x + 3 = 9) é valorada como V.

Uma proposição composta que apresenta em sua tabela-verdade somente V, independentemente das valorações das proposições que a compõem, é denominada logicamente verdadeira ou tautologia. Por exemplo, independentemente das valorações V ou F de uma proposição A, todos os elementos da tabela-verdade da proposição A∨(¬A) são V, isto é, A∨(¬A) é uma tautologia.

Considerando as informações do texto acima, julgue o(s) item(ns):