
A adição é uma das quatro operações básicas da álgebra. Consiste em combinar dois números (chamados de termos, somandos ou parcelas) em um único número, a soma. Para se adicionar mais números, basta repetir a operação. Em termos mais simples, podemos pensar na operação de adição quando nosso desejo é juntar coisas que estão separadas.
Em um colégio, existem 3 turmas. A primeira turma tem 14 alunos, a segunda tem 19 alunos e a terceira tem 15 alunos. Quantos alunos o colégio possui?
Para determinarmos a quantidade de alunos que o colégio possui, basta juntarmos os alunos de todas as turmas. Isto é: somar a quantidade de alunos de cada turma.
14 + 19 + 15 = 48
Portanto, existem 48 alunos neste colégio.
Em seu aniversário de 7 anos, Leonardo recebeu presentes em dinheiro. Seu pai lhe deu R$ 15,50, sua mãe R$ 7,65 e seu irmão R$ 8,28. Qual o valor total recebido por Leonardo?
Para calcularmos o valor total recebido por Leonardo, basta somarmos todos os valores recebidos.
Para realizar a adição de números decimais, as parcelas são dispostas de modo que se tenha vírgula sobre vírgula.

A soma é feita por colunas, da direita para a esquerda. Caso a soma da coluna ultrapasse o valor 9 (nove), somente preencheremos o campo de resultado com o dígito direito do resultado obtido. Os dígitos restantes ficarão acima da coluna imediatamente à esquerda da coluna somada. No caso da coluna somada ser a última, todos os dígitos poderão ser incluídos no campo de resultado.
Neste exemplo, a primeira coluna a ser somada tem os seguintes valores: 0, 5 e 8. Portanto, 0 + 5 + 8 = 13. Como o resultado ultrapassou o valor 9, preencheremos o campo de resultado somente com o o dígito direito do resultado obtido (neste caso, o número 3). O dígito 1 será incluído acima da coluna imediatamente à esquerda da coluna calculada.
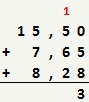
Na segunda coluna, os valores a serem somados incluem o número 1 colocado acima desta coluna. Portanto, 1 + 5 + 6 + 2 = 14. O mesmo procedimento é utilizado até calcularmos todas as colunas, obtendo-se assim a soma desejada.

Com este resultado, sabemos que o valor total recebido por Leonardo é R$ 31,43.
Podemos definir as frações como partes de um todo. Por exemplo, teremos  de uma pizza se dividirmos esta pizza em 8 pedaços iguais e tomarmos 3 destas partes. Também definimos a fração como o
resultado da divisão de dois números. Por exemplo, a fração
de uma pizza se dividirmos esta pizza em 8 pedaços iguais e tomarmos 3 destas partes. Também definimos a fração como o
resultado da divisão de dois números. Por exemplo, a fração  é o resultado da divisão de 3 por 8.
é o resultado da divisão de 3 por 8.
Para somar frações que tenham o mesmo denominador, basta somar seus numeradores, como no exemplo abaixo:
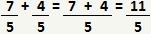
No caso de frações com denominadores diferentes, devemos seguir alguns passos. Para entendermos este processo, calcularemos a seguinte soma de frações:
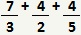
1.º Passo: Encontrar um número que seja múltiplo de todos os denominadores (para isto, podemos utilizar o M.M.C., que será detalhado em outro tópico). Este número será o novo denominador.
Podemos utilizar, neste exemplo, o número 30 como múltiplo de todos os denominadores.
2.º Passo: Representar todas as frações da adição com este mesmo denominador. Para representar cada fração com este novo denominador, basta dividirmos este novo denominador pelo numerador da fração, e então multiplicar o resultado obtido pelo numerador desta mesma fração, obtendo assim o novo numerador desta fração.
Nas frações de nosso exemplo as contas são: 30 ÷ 3 × 7 = 70, 30 ÷ 2 × 4 = 60 e 30 ÷ 5 × 4 = 24. Portanto, temos:
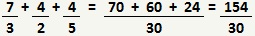
Apenas simplificando, temos:
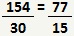
1) Comutatividade: A ordem das parcelas não altera o resultado final da operação. Assim, se x + y = z, logo y + x = z.
2) Associatividade: O agrupamento das parcelas não altera o resultado. Assim, se (x + y) + z = w, logo x + (y + z) = w.
3) Elemento Neutro: A parcela 0 (zero) não altera o resultado das demais parcelas. O zero é chamado "elemento neutro" da adição. Assim, se x + y = z, logo x + y + 0 = z.
4) Fechamento: A soma de dois números naturais será sempre um número natural.
5) Anulação: A soma de qualquer número e o seu oposto é zero. Exemplo: 2 + (-2) = 0.
A subtração pode ser considerada como o oposto da adição. Pensamos em subtração quando queremos tirar um valor de outro, para saber quanto restará. Por exemplo, temos:
a - b = c
Nesta subtração, temos que: a é o minuendo, b é o subtraendo e c é a diferença (ou resto).
Um carteiro, de nome Francisco, deve entregar 100 correspondências por dia. Se em determinado dia, até seu almoço, Francisco entregar 63 correspondências, quantas ele deverá entregar após o almoço para atingir sua meta?
Para determinarmos a quantidade de correspondências que devem ser entregues após o almoço, devemos subtrair o número de correspondências já entregues. Ou seja, subtrair 63 de 100:
100 - 63 = 37
Portanto, Francisco deverá entregar 37 correspondências após o almoço.
Marta foi à feira e levou R$ 43,50. Durante suas compras, Marta gastou 31,23. Com quanto dinheiro Marta voltou para casa?
Para calcularmos o valor restante, basta subtrairmos o valor gasto do valor inicial.
Para realizar a subtração de números decimais, as parcelas são dispostas de modo que se tenha vírgula sobre vírgula.

A subtração é feita por colunas, da direita para a esquerda, onde devemos retirar do dígito do minuendo o dígito do subtraendo. Caso o dígito do minuendo seja menor do que o dígito do subtraendo, devemos retirar uma unidade do dígito do minuendo imediatamente à esquerda do dígito que está sendo calculado, e somar 10 (dez) ao dígito do minuendo do cálculo atual.
Neste exemplo, a primeira coluna a ser subtraída apresenta os seguintes valores: 0 (dígito do minuendo) e 3 (dígito do subtraendo). Como o dígito do minuendo é menor que o dígito do subtraendo, precisamos retirar 1 (um) do dígito do minuendo à esquerda (neste caso, o dígito 5). Após isto, devemos somar 10 (dez) ao dígito do minuendo do cálculo atual. Portanto, o dígito 5 passa a valer 4, e o dígito 0 passa a valer 10. Veja abaixo como ficou a subtração após o cálculo da primeira coluna:

O mesmo procedimento é utilizado até calcularmos todas as colunas, obtendo-se assim a subtração desejada.
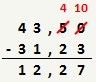
Com este resultado, sabemos que Marta voltou para casa com R$ 12,27.
Para subtrair frações que tenham o mesmo denominador, basta subtrair seus numeradores, como no exemplo abaixo:
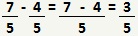
No caso de frações com denominadores diferentes, devemos seguir alguns passos. Para entendermos este processo, calcularemos a seguinte subtração de frações:

1.º Passo: Encontrar um número que seja múltiplo de todos os denominadores (para isto, podemos utilizar o M.M.C., que será detalhado em outro tópico). Este número será o novo denominador.
Podemos utilizar, neste exemplo, o número 30 como múltiplo de todos os denominadores.
2.º Passo: Representar todas as frações da subtração com este mesmo denominador. Para representar cada fração com este novo denominador, basta dividirmos este novo denominador pelo numerador da fração, e então multiplicar o resultado obtido pelo numerador desta mesma fração, obtendo assim o novo numerador desta fração.
Nas frações de nosso exemplo as contas são: 30 ÷ 15 × 13 = 26 e 30 ÷ 2 × 1 = 15. Portanto, temos:
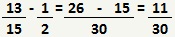
3) Elemento Neutro: A parcela 0 (zero) não altera o resultado das demais parcelas. O zero é chamado "elemento neutro" da adição. Assim, x - 0 = x, y - 0 = y e x - 0 - y = x - y.
4) Fechamento: A diferença de dois números naturais será sempre um número natural.
5) Anulação: Quando o minuendo é igual ao subtraendo, a diferença será 0 (zero). Exemplo: 2 - 2 = 0.
Em sua forma mais simples, a multiplicação nada mais é do que uma simples forma de se somar uma quantidade finita de números iguais. Na multiplicação cada número é chamado de fator, e o resultado da multiplicação é chamado de produto.
A multiplicação pode ser escrita de diversas formas, todas elas equivalentes: 3 × 4 = 3 . 4 = 3 * 4.
A multiplicação de números inteiros pode ser considerada como uma soma de parcelas iguais. Por exemplo:
4 × 3 = 3 + 3 + 3 + 3 = 12
O número 3 apareceu 4 vezes. Portanto, 4 vezes 3 é igual a 12. Da mesma forma temos:
3 × 4 = 4 + 4 + 4 = 12
Neste caso, o número 4 apareceu 3 vezes. Então, 3 vezes 4 é igual a 12.
Problema: Sabemos que Patrícia treina natação durante 45 horas a cada mês. Quantas horas Patrícia treina durante um ano?
Para determinarmos quantas horas de treinamento Patrícia realiza em um ano, devemos multiplicar a quantidade de horas de treinamento em um mês (15) pela quantidade de meses em um ano (12).
Temos, portanto, a seguinte multiplicação a ser realizada: 15 × 12.
Para realizarmos a multiplicação, montamos a conta da seguinte maneira:

Da direita para esquerda, devemos multiplicar cada dígito do segundo fator por todos os dígitos do primeiro fator.
A disposição do resultado se dará da direita para a esquerda, iniciando-se abaixo do dígito do segundo fator que está sendo calculado.
Caso a multiplicação de dois dígitos ultrapasse o valor 9 (nove), somente preencheremos o campo de resultado com o dígito direito do resultado obtido. Os dígitos restantes ficarão acima do dígito do primeiro fator, imediatamente à esquerda do dígito calculado. No caso do dígito da esquerda do primeiro fator, todos os dígitos poderão ser incluídos no campo de resultado.
Neste exemplo, temos a seguinte multiplicação: 2 × 5 = 10. Portanto, o 0 (zero) fica abaixo do 2, e o 1 fica acima do dígito 1 do primeiro fator.
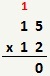
Quando o dígito do primeiro fator estiver sendo multiplicado e tiver herdado um número acima, será feita a multiplicação normalmente, e após isto será somado o valor que estiver acima deste dígito, conforme mostra o exemplo abaixo, onde 2 × 1 + 1 = 3